PyTorch : Linear Regression from scratch¶

Tensors & Gradients¶

A tensor is a number, vector, matrix or any n-dimensional array.

tensor(3.)
tensor(4., requires_grad=True)
tensor(5., requires_grad=True)

We can combine tensors with the usual arithmetic operations.

What makes PyTorch special, is that we can automatically compute the derivative of y w.r.t. the tensors that have requires_grad set to True i.e. w and b.

dy/dw: tensor(3.)
dy/db: tensor(1.)

Before we build a model, we need to convert inputs and targets to PyTorch tensors.

Linear Regression Model (from scratch)¶

The weights and biases can also be represented as matrices, initialized with random values. The first row of w and the first element of b are use to predict the first target variable i.e. yield for apples, and similarly the second for oranges.

tensor([[-0.8733, -0.1805,  0.5345],
        [ 0.7049,  1.1042,  0.6289]], requires_grad=True)
tensor([-0.3664,  0.1522], requires_grad=True)

The model is simply a function that performs a matrix multiplication of the input x and the weights w (transposed) and adds the bias b (replicated for each observation).

X×WT+bX×WT+b⎡⎢ ⎢ ⎢ ⎢⎣736743918864⋮⋮⋮699670⎤⎥ ⎥ ⎥ ⎥⎦×⎡⎢⎣w11w21w12w22w13w23⎤⎥⎦+⎡⎢ ⎢ ⎢ ⎢⎣b1b2b1b2⋮⋮b1b2⎤⎥ ⎥ ⎥ ⎥⎦[736743918864⋮⋮⋮699670]×[w11w21w12w22w13w23]+[b1b2b1b2⋮⋮b1b2]

The matrix obtained by passing the input data to the model is a set of predictions for the target variables.

Because we've started with random weights and biases, the model does not a very good job of predicting the target varaibles.

Loss Function¶

We can compare the predictions with the actual targets, using the following method:

  • Calculate the difference between the two matrices (preds and targets).
  • Square all elements of the difference matrix to remove negative values.
  • Calculate the average of the elements in the resulting matrix.

The result is a single number, known as the mean squared error (MSE).

tensor(14555.1924, grad_fn=<DivBackward0>)

The resulting number is called the loss, because it indicates how bad the model is at predicting the target variables. Lower the loss, better the model.

Compute Gradients¶

With PyTorch, we can automatically compute the gradient or derivative of the loss w.r.t. to the weights and biases, because they have requires_grad set to True.

The gradients are stored in the .grad property of the respective tensors.

tensor([[-0.8733, -0.1805,  0.5345],
        [ 0.7049,  1.1042,  0.6289]], requires_grad=True)
tensor([[-11477.6719, -12635.1074,  -7695.5312],
        [  8263.8701,   8348.2227,   5209.8843]])

tensor([-0.3664,  0.1522], requires_grad=True)
tensor([-136.6430,   96.3747])

A key insight from calculus is that the gradient indicates the rate of change of the loss, or the slope of the loss function w.r.t. the weights and biases.

  • If a gradient element is postive,
    • increasing the element's value slightly will increase the loss.
    • decreasing the element's value slightly will decrease the loss.

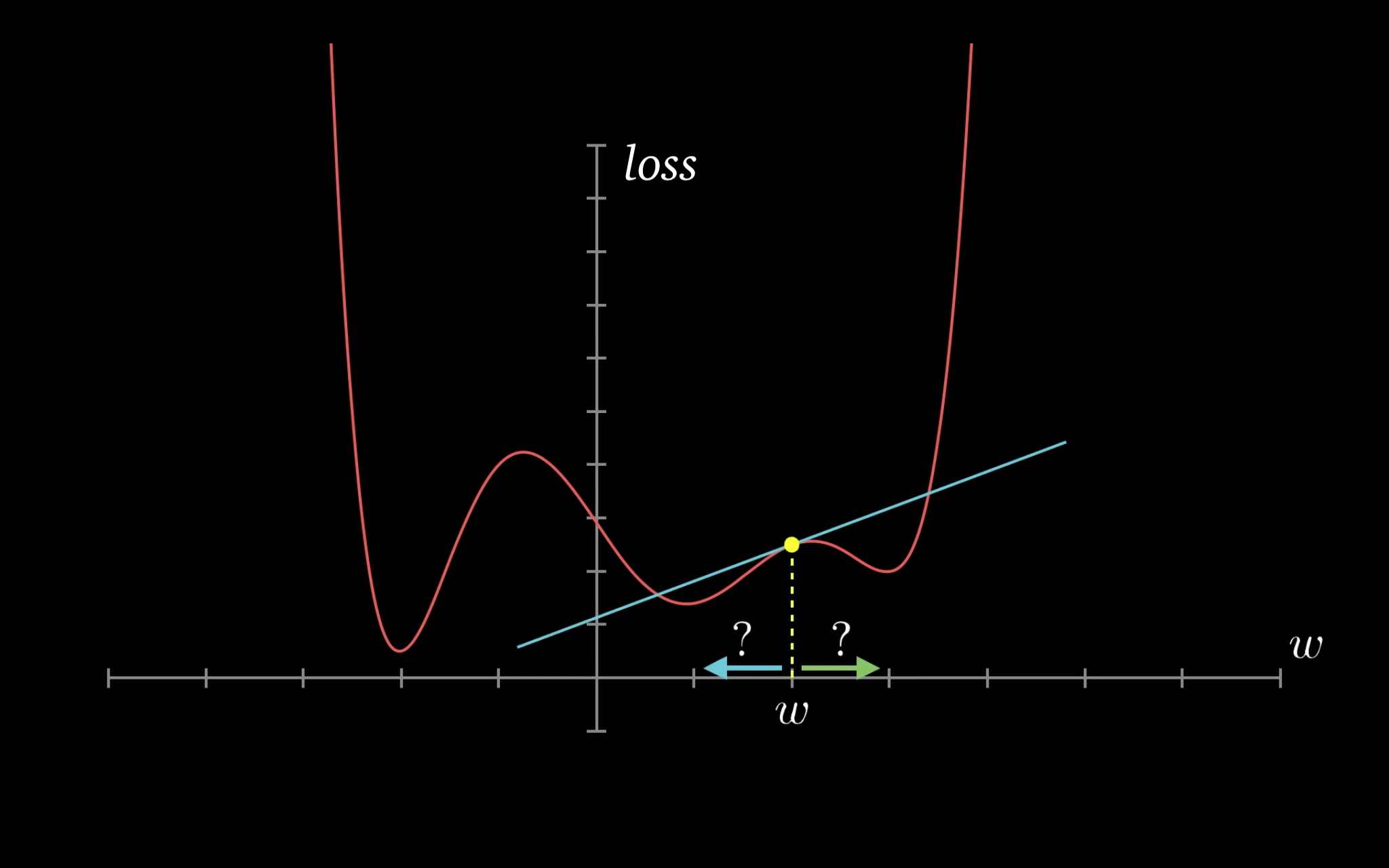
  • If a gradient element is negative,
    • increasing the element's value slightly will decrease the loss.
    • decreasing the element's value slightly will increase the loss.

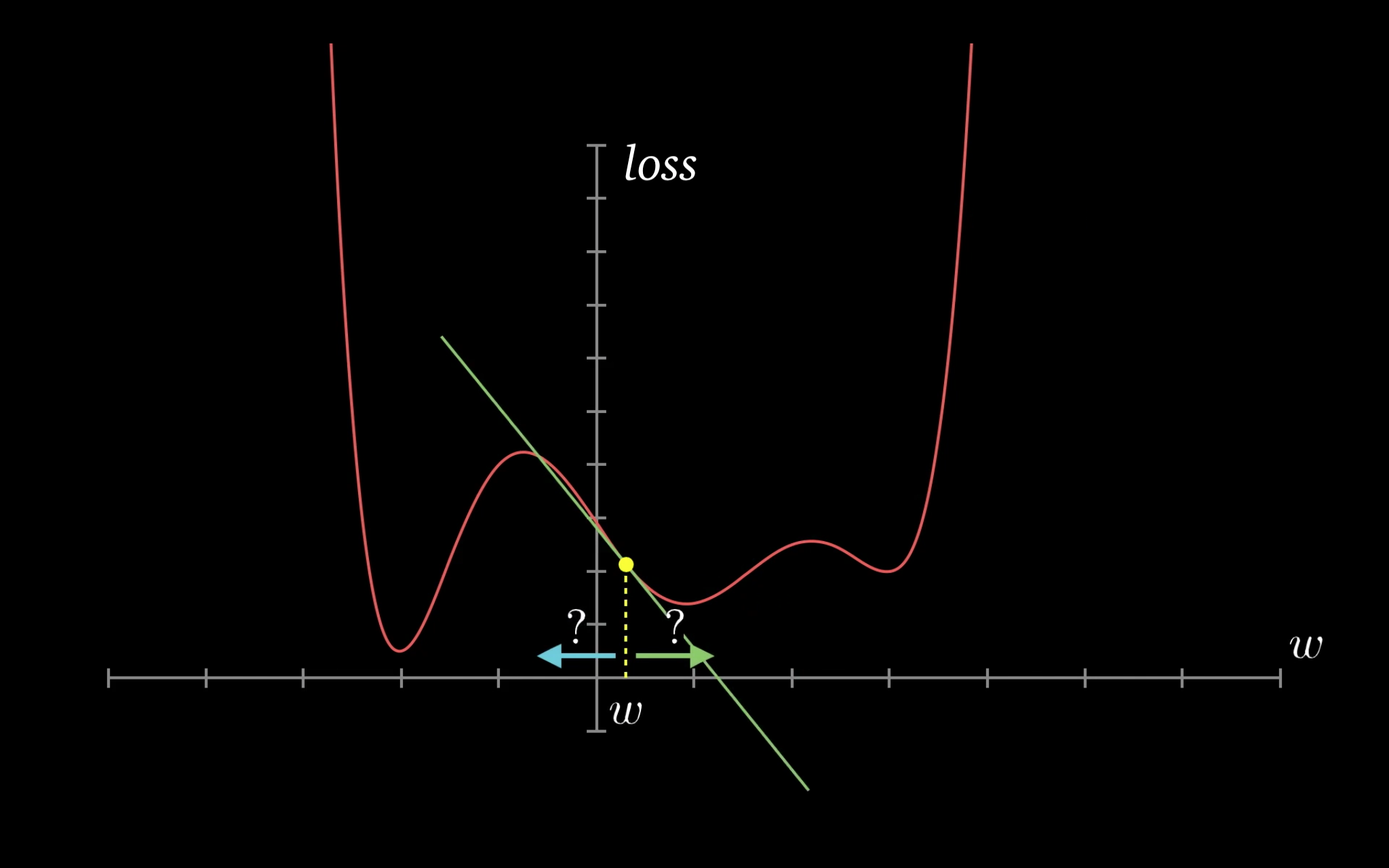
The increase or decrease is proportional to the value of the gradient.

Finally, we'll reset the gradients to zero before moving forward, because PyTorch accumulates gradients.

Adjust weights and biases using gradient descent¶

We'll reduce the loss and improve our model using the gradient descent algorithm, which has the following steps:

  1. Generate predictions
  2. Calculate the loss
  3. Compute gradients w.r.t the weights and biases
  4. Adjust the weights by subtracting a small quantity proportional to the gradient
  5. Reset the gradients to zero

With the new weights and biases, the model should have a lower loss.

Train for multiple epochs¶

To reduce the loss further, we repeat the process of adjusting the weights and biases using the gradients multiple times. Each iteration is called an epoch.

Linear Regression Model using PyTorch built-ins¶

Let's re-implement the same model using some built-in functions and classes from PyTorch.

Out[3]:
Unnamed: 0 Date_excel Rainfall_Terni Flow_Rate_Lupa doy Month Year ET01 Infilt_ Infiltsum ... log_Flow_diff Flow_saturation Flow_Rate_diff2 log_Flow_diff2 Nera Nera40 Flow_Rate_40 Rainfall_40 Rainfall_240 Rainfall_720
2010-01-01 2010-01-01 2010-01-01 40.8 82.24 1.0 1.0 2010.0 1.338352 1.934648 1.934648 ... 0.077870 3.891051 4.66 0.077870 0.9 0.8000 114.45800 141.000000 221.100003 555.600006
2010-01-02 2010-01-02 2010-01-02 6.8 88.90 2.0 1.0 2010.0 1.701540 1.571460 3.506108 ... 0.077870 3.599550 4.66 0.051091 1.2 0.8000 114.45800 141.000000 227.900003 562.400006
2010-01-03 2010-01-03 2010-01-03 0.0 93.56 3.0 1.0 2010.0 0.938761 2.334239 5.840347 ... 0.051091 3.420265 11.32 0.128961 0.7 0.8000 114.45800 141.000000 227.900003 562.400006
2010-01-04 2010-01-04 2010-01-04 4.2 96.63 4.0 1.0 2010.0 0.996871 2.276129 8.116476 ... 0.032286 3.311601 7.73 0.083377 0.6 0.8000 114.45800 141.000000 232.100003 566.600006
2010-01-05 2010-01-05 2010-01-05 26.0 98.65 5.0 1.0 2010.0 1.278242 1.994758 10.111234 ... 0.020689 3.243791 5.09 0.052975 0.6 0.8000 114.45800 141.000000 255.600003 592.600006
... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...
2020-06-25 2020-06-25 2020-06-25 0.0 74.29 177.0 6.0 2020.0 4.030210 -4.030210 -541.652567 ... -0.003896 4.307444 -0.59 -0.007910 0.4 0.4100 80.97475 86.100001 526.800009 1557.300026
2020-06-26 2020-06-26 2020-06-26 0.0 73.93 178.0 6.0 2020.0 4.171681 -4.171681 -545.824247 ... -0.004858 4.328419 -0.65 -0.008754 0.4 0.4100 80.62650 86.100001 526.800009 1557.300026
2020-06-27 2020-06-27 2020-06-27 0.0 73.60 179.0 6.0 2020.0 4.449783 -4.449783 -550.274031 ... -0.004474 4.347826 -0.69 -0.009331 0.4 0.4100 80.28100 86.100001 522.300009 1557.300026
2020-06-28 2020-06-28 2020-06-28 0.0 73.14 180.0 6.0 2020.0 4.513588 -4.513588 -554.787618 ... -0.006270 4.375171 -0.79 -0.010743 0.4 0.4075 79.93350 86.100001 520.600009 1557.300026
2020-06-29 2020-06-29 2020-06-29 0.0 72.88 181.0 6.0 2020.0 4.510906 -4.510906 -559.298525 ... -0.003561 4.390779 -0.72 -0.009831 0.4 0.4075 79.58650 71.000000 512.500009 1557.300026

3833 rows × 57 columns

Out[4]:
Index(['Unnamed: 0', 'Date_excel', 'Rainfall_Terni', 'Flow_Rate_Lupa', 'doy',
       'Month', 'Year', 'ET01', 'Infilt_', 'Infiltsum', 'Rainfall_Ter', 'P5',
       'Flow_Rate_Lup', 'Infilt_m3', 'Week', 'log_Flow', 'Lupa_Mean99_2011',
       'Rainfall_Terni_minET', 'Infiltrate', 'log_Flow_10d', 'log_Flow_20d',
       'α10', 'α20', 'log_Flow_10d_dif', 'log_Flow_20d_dif', 'α10_30',
       'Infilt_7YR', 'Infilt_2YR', 'α1', 'α1_negatives', 'ro', 'Infilt_M6',
       'filtered_Infilt_M6', 'Rainfall_Terni_scale_12_calculated_index',
       'SMroot', 'Neradebit', 'smian', 'DroughtIndex', 'Deficit', 'PET_hg',
       'GWETTOP', 'V_sq2gh', 'Unix_ts', 'rr', 'pp', 'log_Rainfall',
       'Flow_Rate_diff', 'log_Flow_diff', 'Flow_saturation', 'Flow_Rate_diff2',
       'log_Flow_diff2', 'Nera', 'Nera40', 'Flow_Rate_40', 'Rainfall_40',
       'Rainfall_240', 'Rainfall_720'],
      dtype='object')
Out[59]:
Unnamed: 0 Date_excel Rainfall_Terni Flow_Rate_Lupa doy Month Year ET01 Infilt_ Infiltsum ... log_Flow_diff Flow_saturation Flow_Rate_diff2 log_Flow_diff2 Nera Nera40 Flow_Rate_40 Rainfall_40 Rainfall_240 Rainfall_720
2010-01-01 2010-01-01 2010-01-01 40.8 82.24 1.0 1.0 2010.0 1.338352 1.934648 1.934648 ... 0.077870 3.891051 4.66 0.077870 0.9 0.800000 114.458000 141.0 221.100003 555.600006
2010-01-02 2010-01-02 2010-01-02 6.8 88.90 2.0 1.0 2010.0 1.701540 1.571460 3.506108 ... 0.077870 3.599550 4.66 0.051091 1.2 0.800000 114.458000 141.0 227.900003 562.400006
2010-01-03 2010-01-03 2010-01-03 0.0 93.56 3.0 1.0 2010.0 0.938761 2.334239 5.840347 ... 0.051091 3.420265 11.32 0.128961 0.7 0.800000 114.458000 141.0 227.900003 562.400006
2010-01-04 2010-01-04 2010-01-04 4.2 96.63 4.0 1.0 2010.0 0.996871 2.276129 8.116476 ... 0.032286 3.311601 7.73 0.083377 0.6 0.800000 114.458000 141.0 232.100003 566.600006
2010-01-05 2010-01-05 2010-01-05 26.0 98.65 5.0 1.0 2010.0 1.278242 1.994758 10.111234 ... 0.020689 3.243791 5.09 0.052975 0.6 0.800000 114.458000 141.0 255.600003 592.600006
2010-01-06 2010-01-06 2010-01-06 18.0 102.15 6.0 1.0 2010.0 1.212833 2.060167 12.171402 ... 0.034864 3.132648 5.52 0.055553 0.9 0.816667 114.458000 141.0 273.600003 610.600006
2010-01-07 2010-01-07 2010-01-07 12.0 106.57 7.0 1.0 2010.0 1.230956 2.042044 14.213446 ... 0.042360 3.002721 7.92 0.077224 0.8 0.814286 114.458000 141.0 276.000003 622.600006
2010-01-08 2010-01-08 2010-01-08 25.6 110.57 8.0 1.0 2010.0 1.495457 1.777543 15.990988 ... 0.036847 2.894094 8.42 0.079206 0.6 0.787500 114.458000 141.0 285.500002 648.200006
2010-01-09 2010-01-09 2010-01-09 5.4 117.00 9.0 1.0 2010.0 1.147559 2.125441 18.116429 ... 0.056525 2.735043 10.43 0.093372 0.7 0.777778 114.458000 141.0 286.800002 653.600006
2010-01-10 2010-01-10 2010-01-10 0.2 124.15 10.0 1.0 2010.0 1.080884 2.192116 20.308545 ... 0.059317 2.577527 13.58 0.115842 0.7 0.770000 114.458000 141.0 282.900002 653.800006
2010-01-11 2010-01-11 2010-01-11 1.6 130.30 11.0 1.0 2010.0 1.044000 2.229000 22.537545 ... 0.048349 2.455871 13.30 0.107666 0.7 0.763636 114.458000 141.0 267.300002 655.400006
2010-01-12 2010-01-12 2010-01-12 0.4 135.60 12.0 1.0 2010.0 1.172074 2.100926 24.638471 ... 0.039870 2.359882 11.45 0.088219 0.6 0.750000 114.458000 141.0 241.100001 655.800006
2010-01-13 2010-01-13 2010-01-13 0.0 140.13 13.0 1.0 2010.0 1.062407 2.210593 26.849063 ... 0.032861 2.283594 9.83 0.072731 0.6 0.738462 114.458000 141.0 233.800001 655.800006
2010-01-14 2010-01-14 2010-01-14 0.0 143.60 14.0 1.0 2010.0 1.257670 2.015330 28.864393 ... 0.024461 2.228412 8.00 0.057322 0.6 0.728571 114.458000 141.0 219.200001 655.800006
2010-01-15 2010-01-15 2010-01-15 0.0 146.82 15.0 1.0 2010.0 1.237920 2.035080 30.899473 ... 0.022176 2.179540 6.69 0.046637 0.6 0.720000 114.458000 141.0 212.100001 655.800006
2010-01-16 2010-01-16 2010-01-16 0.0 149.64 16.0 1.0 2010.0 1.137734 2.135266 33.034739 ... 0.019025 2.138466 6.04 0.041201 0.6 0.712500 116.656875 141.0 206.500001 655.800006
2010-01-17 2010-01-17 2010-01-17 2.6 152.13 17.0 1.0 2010.0 1.153557 2.119443 35.154182 ... 0.016503 2.103464 5.31 0.035528 0.6 0.705882 118.743529 143.6 209.100001 658.400006
2010-01-18 2010-01-18 2010-01-18 0.0 153.59 18.0 1.0 2010.0 1.379578 1.893422 37.047603 ... 0.009551 2.083469 3.95 0.026054 0.6 0.700000 120.679444 143.6 209.100001 658.400006
2010-01-19 2010-01-19 2010-01-19 0.0 154.92 19.0 1.0 2010.0 1.135630 2.137370 39.184973 ... 0.008622 2.065582 2.79 0.018173 0.6 0.694737 122.481579 143.6 209.100001 658.400006
2010-01-20 2010-01-20 2010-01-20 0.0 155.98 20.0 1.0 2010.0 1.222036 2.050964 41.235937 ... 0.006819 2.051545 2.39 0.015441 0.6 0.690000 124.156500 143.6 209.100001 658.400006
2010-01-21 2010-01-21 2010-01-21 0.0 156.60 21.0 1.0 2010.0 1.061965 2.211035 43.446972 ... 0.003967 2.043423 1.68 0.010786 0.6 0.685714 125.701429 143.6 209.100001 658.400006
2010-01-22 2010-01-22 2010-01-22 0.0 157.40 22.0 1.0 2010.0 0.904019 2.368981 45.815953 ... 0.005096 2.033037 1.42 0.009063 0.6 0.681818 127.142273 143.6 209.100001 658.400006
2010-01-23 2010-01-23 2010-01-23 0.0 157.56 23.0 1.0 2010.0 0.917046 2.355954 48.171907 ... 0.001016 2.030972 0.96 0.006112 0.6 0.678261 128.464783 143.6 209.100001 658.400006
2010-01-24 2010-01-24 2010-01-24 0.0 157.79 24.0 1.0 2010.0 1.195283 2.077717 50.249625 ... 0.001459 2.028012 0.39 0.002475 0.6 0.675000 129.686667 143.6 209.100001 658.400006
2010-01-25 2010-01-25 2010-01-25 0.8 158.08 25.0 1.0 2010.0 1.079597 2.193403 52.443028 ... 0.001836 2.024291 0.52 0.003295 0.6 0.672000 130.822400 144.4 209.900001 659.200006
2010-01-26 2010-01-26 2010-01-26 20.0 158.23 26.0 1.0 2010.0 0.662108 2.610892 55.053919 ... 0.000948 2.022372 0.44 0.002785 0.6 0.669231 131.876538 164.4 229.900001 679.200006
2010-01-27 2010-01-27 2010-01-27 0.0 158.19 27.0 1.0 2010.0 1.025926 2.247074 57.300993 ... -0.000253 2.022884 0.11 0.000696 0.6 0.666667 132.851111 164.4 229.900001 679.200006
2010-01-28 2010-01-28 2010-01-28 0.2 158.41 28.0 1.0 2010.0 1.076166 2.196834 59.497827 ... 0.001390 2.020074 0.18 0.001137 0.6 0.664286 133.763929 164.6 230.100001 679.400006
2010-01-29 2010-01-29 2010-01-29 2.2 158.52 29.0 1.0 2010.0 1.184512 2.088488 61.586315 ... 0.000694 2.018673 0.33 0.002084 0.6 0.662069 134.617586 166.8 232.300001 681.600006
2010-01-30 2010-01-30 2010-01-30 18.4 158.42 30.0 1.0 2010.0 1.231948 2.041052 63.627367 ... -0.000631 2.019947 0.01 0.000063 0.6 0.660000 135.411000 185.2 250.700001 700.000006
2010-01-31 2010-01-31 2010-01-31 2.6 159.86 31.0 1.0 2010.0 1.014567 2.258433 65.885799 ... 0.009049 2.001752 1.34 0.008418 0.6 0.658065 136.199677 187.8 244.600001 702.600006
2010-02-01 2010-02-01 2010-02-01 0.8 160.88 32.0 2.0 2010.0 0.738966 3.000034 68.885833 ... 0.006360 1.989060 2.46 0.015409 0.6 0.656250 136.970937 188.6 225.100000 703.400006
2010-02-02 2010-02-02 2010-02-02 0.0 161.93 33.0 2.0 2010.0 0.916826 2.822174 71.708007 ... 0.006505 1.976163 2.07 0.012866 0.6 0.654545 137.727273 188.6 225.100000 703.400006
2010-02-03 2010-02-03 2010-02-03 0.0 162.60 34.0 2.0 2010.0 1.357302 2.381698 74.089705 ... 0.004129 1.968020 1.72 0.010634 0.6 0.652941 138.458824 188.6 207.100000 703.400006
2010-02-04 2010-02-04 2010-02-04 0.0 163.02 35.0 2.0 2010.0 1.459571 2.279429 76.369134 ... 0.002580 1.962949 1.09 0.006709 0.6 0.651429 139.160571 188.6 195.400000 703.400006
2010-02-05 2010-02-05 2010-02-05 20.4 163.94 36.0 2.0 2010.0 1.499494 2.239506 78.608640 ... 0.005628 1.951934 1.34 0.008207 0.6 0.650000 139.848889 209.0 209.000000 723.800006
2010-02-06 2010-02-06 2010-02-06 13.4 165.07 37.0 2.0 2010.0 1.170890 2.568110 81.176750 ... 0.006869 1.938572 2.05 0.012497 0.7 0.651351 140.530541 222.4 222.400000 737.200006
2010-02-07 2010-02-07 2010-02-07 0.2 167.30 38.0 2.0 2010.0 1.086957 2.652043 83.828793 ... 0.013419 1.912732 3.36 0.020288 0.7 0.652632 141.235000 222.6 222.600000 737.400006
2010-02-08 2010-02-08 2010-02-08 0.0 169.25 39.0 2.0 2010.0 0.992749 2.746251 86.575044 ... 0.011588 1.890694 4.18 0.025007 0.6 0.651282 141.953333 222.6 222.600000 737.400006
2010-02-09 2010-02-09 2010-02-09 2.4 171.34 40.0 2.0 2010.0 1.201026 2.537974 89.113017 ... 0.012273 1.867632 4.04 0.023861 0.6 0.650000 142.688000 225.0 225.000000 739.800006
2010-02-10 2010-02-10 2010-02-10 12.4 173.38 41.0 2.0 2010.0 1.181394 2.557606 91.670624 ... 0.011836 1.845657 4.13 0.024109 0.6 0.642500 144.966500 196.6 237.400000 752.200006
2010-02-11 2010-02-11 2010-02-11 1.2 175.02 42.0 2.0 2010.0 1.181061 2.557939 94.228563 ... 0.009415 1.828362 3.68 0.021250 0.6 0.627500 147.119500 191.0 238.600000 753.400006
2010-02-12 2010-02-12 2010-02-12 1.4 177.10 43.0 2.0 2010.0 1.015194 2.723806 96.952369 ... 0.011814 1.806889 3.72 0.021229 0.6 0.625000 149.208000 192.4 240.000000 754.800006
2010-02-13 2010-02-13 2010-02-13 1.6 178.77 44.0 2.0 2010.0 1.218784 2.520216 99.472584 ... 0.009386 1.790010 3.75 0.021200 0.6 0.625000 151.261500 189.8 241.600000 756.400006
2010-02-14 2010-02-14 2010-02-14 0.0 180.19 45.0 2.0 2010.0 1.265581 2.473419 101.946003 ... 0.007912 1.775903 3.09 0.017297 0.5 0.622500 153.300000 163.8 241.600000 756.400006

45 rows × 57 columns

seems like a combination of a weibull and bimodal distribution.

Out[81]:
(3833, 14) (3833, 1) float64 float64 <class 'numpy.ndarray'>

Dataset and DataLoader¶

We'll create a TensorDataset, which allows access to rows from inputs and targets as tuples. We'll also create a DataLoader, to split the data into batches while training. It also provides other utilities like shuffling and sampling.

Out[10]:
(tensor([[-4.3338e+00, -1.4120e+00, -1.5607e+00, -6.6982e-01,  4.6013e+00,
           4.4589e+00,  7.0096e-01,  4.3845e-01, -5.0115e-01, -1.3594e+00,
           6.0583e+00, -5.9594e-06, -2.1739e+00,  5.0134e-01],
         [-4.3111e+00, -1.4125e+00, -1.5607e+00, -6.7003e-01,  8.0048e+00,
           4.4589e+00,  7.1636e-01,  4.3844e-01, -5.0115e-01, -7.8222e-01,
           6.5504e-01, -5.9594e-06, -2.1380e+00,  5.0134e-01]]),
 tensor([[-0.4095],
         [-0.2648]]))
Out[11]:

nn.Linear¶

Instead of initializing the weights & biases manually, we can define the model using nn.Linear.

Parameter containing:
tensor([[-0.0360, -0.2029,  0.2390,  0.0867,  0.2527, -0.0131,  0.1957, -0.0834,
          0.1752, -0.2113, -0.1763,  0.1826,  0.1889,  0.1053]],
       requires_grad=True)
Parameter containing:
tensor([-0.0010], requires_grad=True)

Optimizer¶

Instead of manually manipulating the weights & biases using gradients, we can use the optimizer optim.SGD.

Loss Function¶

Instead of defining a loss function manually, we can use the built-in loss function mse_loss.

loss = loss_fn(model(inputs), targets) print(loss)

Train the model¶

We are ready to train the model now. We can define a utility function fit which trains the model for a given number of epochs.

Out[39]:
tensor([[-0.2232],
        [-1.3376],
        [-0.6210],
        ...,
        [ 0.6464],
        [ 0.6729],
        [ 0.6763]], grad_fn=<AddmmBackward0>)
Out[40]:

Reset model weights¶

Out[48]:
Linear(in_features=14, out_features=1, bias=True)

Feedforward Neural Network¶

ffnn

Conceptually, you think of feedforward neural networks as two or more linear regression models stacked on top of one another with a non-linear activation function applied between them.

To use a feedforward neural network instead of linear regression, we can extend the nn.Module class from PyTorch.

Now we can define the model, optimizer and loss function exactly as before.

Finally, we can apply gradient descent to train the model using the same fit function defined earlier for linear regression. (mind it uses train_dl !!)

import or start tensorboard:¶

  • via cmd (in case tensorboard is installed in a conda virt. env.) , or
  • via notebook line magic

conda activate keras

cd "C:\Users\VanOp\Documents\Notebooks\torch\"

tensorboard --logdir runs/Lupa_water_spring_experiment_1

tracking the model training (of images) with TensorBoard¶

Let's train the SimpleNet for 100 epochs:

Training loss:  tensor(0.1921, grad_fn=<MseLossBackward0>)
Out[22]:
tensor([[ 0.0438],
        [ 1.0782],
        [ 0.2185],
        ...,
        [ 0.1161],
        [-0.2429],
        [-0.1825]], grad_fn=<AddmmBackward0>)

scatterplot for comparing targets and predictions¶

calculate the r2 score, mean_squared_error¶

r2_score: 0.8096 mean_squared_error: 0.05519576843440605

{('linear1.weight', Parameter containing:
tensor([[-0.2174, -0.0477,  0.2296, -0.1854, -0.0897, -0.3259,  0.3711,  0.2363,
         -0.2432, -0.0459, -0.2803,  0.3055, -0.5518, -0.0377],
        [-0.1620, -0.0455,  0.4977, -0.1960,  0.1284, -0.1358,  0.0711,  0.1784,
         -0.0842, -0.1122,  0.2479,  0.1767, -0.0245, -0.1172],
        [ 0.1470, -0.0213,  0.2368,  0.0958,  0.0787,  0.3669,  0.3339,  0.2583,
          0.2184, -0.3127,  0.1844, -0.2393,  0.1190, -0.3780],
        [-0.2335, -0.4764, -0.2744, -0.4631,  0.3320, -0.3015, -0.4802, -0.1977,
          0.3239, -0.2276,  0.0225,  0.2525, -0.0237, -0.1719],
        [-0.0829,  0.4307, -0.0146, -0.0816, -0.4764,  0.2676, -0.3845,  0.0192,
         -0.0333, -0.3748,  0.2229, -0.2139,  0.4690, -0.3792],
        [ 0.0107,  0.0662,  0.5012,  0.2476,  0.0143, -0.3019, -0.3472, -0.3025,
         -0.0371, -0.2818, -0.4075,  0.3411,  0.1113, -0.1859],
        [ 0.4187,  0.1496,  0.1810, -0.2980, -0.1732,  0.3150, -0.2772, -0.2243,
         -0.3606, -0.2044, -0.2539, -0.1795, -0.2794, -0.3949],
        [ 0.5943,  0.1195, -0.0291,  0.0088, -0.3794,  0.0766,  0.0711,  0.0794,
          0.0738,  0.0326, -0.3712,  0.3287,  0.0117,  0.2911],
        [ 0.1236,  0.0750, -0.0046,  0.0852,  0.0744,  0.4183,  0.3072, -0.2120,
         -0.4209,  0.0723, -0.3576,  0.3874,  0.4331, -0.3799],
        [ 0.4258,  0.3015,  0.2174,  0.1015, -0.3777,  0.2987,  0.0797,  0.1690,
         -0.1784,  0.2900,  0.2812,  0.2837, -0.1835, -0.0399],
        [-0.2470, -0.1502,  0.1117, -0.4598,  0.3388, -0.0656,  0.2639,  0.3155,
          0.2992,  0.1453, -0.1092,  0.3163,  0.6282,  0.3293],
        [-0.0649,  0.4257, -0.3316,  0.0303, -0.1931,  0.2408, -0.4654,  0.2061,
          0.2694,  0.1945, -0.3103, -0.3968,  0.0809, -0.2380],
        [-0.1983, -0.2313, -0.2305,  0.1027, -0.0205, -0.1703, -0.0589, -0.3306,
         -0.0739, -0.2513,  0.2541,  0.2837,  0.5314,  0.2525],
        [ 0.0582,  0.1564,  0.4340,  0.0440,  0.0998,  0.2344, -0.4467,  0.1417,
         -0.1391, -0.0632, -0.0043,  0.2358,  0.2559,  0.1380]],
       requires_grad=True)), ('linear5.bias', Parameter containing:
tensor([-0.1055], requires_grad=True)), ('linear4.weight', Parameter containing:
tensor([[ 0.1714,  0.1197,  0.0330,  0.1618, -0.2151,  0.1414,  0.1899,  0.1656,
         -0.0549,  0.2844, -0.0739, -0.2121, -0.0520,  0.0149],
        [ 0.2081, -0.2049, -0.0494, -0.0862,  0.1835,  0.1723,  0.2691,  0.2454,
         -0.1328,  0.2680,  0.1822, -0.1541,  0.2091,  0.2039],
        [ 0.0082,  0.1312, -0.1129, -0.0305, -0.1256, -0.1301, -0.0060,  0.2429,
          0.2288,  0.0901, -0.1780, -0.2241,  0.0952,  0.1636],
        [-0.1290, -0.1019,  0.2428, -0.1472, -0.0250,  0.0081,  0.2377,  0.0191,
         -0.0550, -0.0321, -0.2413,  0.0807,  0.0926, -0.1268],
        [ 0.1914, -0.0724,  0.0591, -0.0411,  0.1717,  0.0010,  0.0359,  0.2572,
         -0.1532, -0.2171,  0.1327, -0.0515,  0.2842, -0.3202],
        [ 0.1614,  0.0544, -0.2580,  0.0157,  0.0379,  0.0778, -0.1868,  0.2161,
         -0.0525, -0.2308,  0.1820,  0.0329, -0.1009,  0.1778],
        [-0.0903, -0.1353, -0.2056, -0.2771,  0.2050,  0.1043, -0.0293,  0.1621,
         -0.1869,  0.1222,  0.2350,  0.1508, -0.1821,  0.2834],
        [ 0.2688, -0.0510,  0.1625, -0.1706, -0.2369,  0.0368, -0.2710,  0.1567,
          0.2810, -0.1745, -0.2284, -0.0040, -0.1609,  0.0600],
        [ 0.1307,  0.0658,  0.0721,  0.2496, -0.0610,  0.1338,  0.1015,  0.0185,
          0.1613,  0.2644, -0.0798, -0.0863,  0.2370,  0.2095],
        [ 0.2089,  0.2733,  0.0730,  0.2533,  0.0299, -0.0084, -0.1657, -0.1189,
         -0.2565,  0.1682,  0.2050, -0.0829, -0.2530, -0.0889],
        [ 0.1045,  0.1494,  0.1488,  0.0423, -0.0553,  0.2152,  0.1122,  0.2012,
         -0.2202,  0.1824, -0.0763, -0.0237, -0.2069,  0.0269],
        [-0.0013, -0.2133, -0.0338,  0.0984,  0.1568, -0.2447,  0.0426,  0.0012,
          0.0676, -0.1821,  0.2396,  0.2206,  0.3121, -0.2286],
        [ 0.1062, -0.1704,  0.1417, -0.2392, -0.0706, -0.2622, -0.0825,  0.1712,
         -0.0053, -0.2546, -0.1470, -0.1186,  0.1783,  0.1717],
        [ 0.1974,  0.2851,  0.2093,  0.0514, -0.0472,  0.2102, -0.3419,  0.1228,
          0.1453,  0.0385,  0.2584, -0.1215, -0.1840, -0.2062]],
       requires_grad=True)), ('linear4.bias', Parameter containing:
tensor([ 0.1178, -0.0455,  0.1218,  0.1181,  0.2027, -0.2611, -0.1499,  0.0352,
         0.0837,  0.1989, -0.0953,  0.2590,  0.0767,  0.1373],
       requires_grad=True)), ('linear3.bias', Parameter containing:
tensor([-0.0025, -0.0077, -0.0057, -0.0073,  0.0109, -0.0125,  0.0121,  0.0202,
        -0.0285,  0.0046,  0.0167, -0.0016,  0.0065,  0.0130],
       requires_grad=True)), ('linear2.weight', Parameter containing:
tensor([[-0.1420,  0.3804,  0.4161,  0.3425,  0.2254,  0.0583, -0.0991,  0.4611,
          0.1529,  0.2844, -0.3813,  0.0910,  0.1286,  0.4384],
        [ 0.2896, -0.1127, -0.1398,  0.1135, -0.1619, -0.2175,  0.1935,  0.0836,
         -0.0041,  0.0473,  0.0014, -0.0691, -0.3158, -0.1613],
        [-0.3189, -0.2332,  0.2725, -0.1830,  0.4944, -0.0563, -0.1150, -0.2143,
          0.4754, -0.3354,  0.3835,  0.2301,  0.3723, -0.3633],
        [-0.2627, -0.1276,  0.0659,  0.1132, -0.1190, -0.4603, -0.2060,  0.3041,
          0.3216, -0.1978,  0.1061,  0.3034, -0.1455,  0.3624],
        [-0.0100, -0.1756,  0.0884, -0.2744,  0.0583,  0.4709,  0.0184, -0.1844,
         -0.0956, -0.0988, -0.2589, -0.4324,  0.3199, -0.3993],
        [ 0.2218, -0.3123, -0.1992,  0.2801, -0.1229,  0.4241,  0.2832,  0.2738,
          0.1238,  0.0352, -0.0678, -0.4130,  0.4317, -0.3584],
        [-0.0341, -0.1671,  0.0178,  0.3847,  0.0790, -0.0114, -0.0334, -0.2519,
         -0.3461,  0.0279, -0.2257,  0.0119, -0.1657,  0.0379],
        [-0.3844, -0.0326, -0.1544, -0.4082,  0.3465,  0.0098,  0.2029, -0.0744,
          0.4221,  0.4238,  0.3138,  0.1537, -0.3871,  0.3048],
        [-0.0310, -0.2871,  0.2842, -0.4538, -0.1230,  0.4883, -0.3638,  0.3351,
          0.2214,  0.1306, -0.0591, -0.3494, -0.0655, -0.3938],
        [-0.2617,  0.3005,  0.4206,  0.0813, -0.1321, -0.3644, -0.2966, -0.0610,
          0.2565, -0.4343,  0.2658, -0.3859, -0.0156,  0.0210],
        [ 0.4863,  0.1667,  0.3306,  0.0689, -0.4304,  0.2662, -0.0058, -0.2870,
          0.1544, -0.0011, -0.3980,  0.3091,  0.2165, -0.2811],
        [ 0.2488,  0.3122,  0.0024,  0.4402, -0.1951,  0.2958, -0.2055, -0.3801,
         -0.1868, -0.0132, -0.1687,  0.1677, -0.0345,  0.0715],
        [ 0.3554,  0.4615,  0.0218,  0.0107,  0.0345,  0.2140,  0.1369, -0.1263,
         -0.3384, -0.3234, -0.0824, -0.1884, -0.2340,  0.1700],
        [-0.1189,  0.3436,  0.4470, -0.4101,  0.4641,  0.1861,  0.3777,  0.0709,
         -0.2931, -0.1375,  0.0879, -0.4039,  0.1675,  0.3870]],
       requires_grad=True)), ('linear1.bias', Parameter containing:
tensor([-0.0010,  0.0032,  0.0196, -0.0214, -0.0005,  0.0027, -0.0052,  0.0170,
         0.0078, -0.0191,  0.0115, -0.0210,  0.0071, -0.0034],
       requires_grad=True)), ('linear2.bias', Parameter containing:
tensor([ 0.0054,  0.0212,  0.0157,  0.0018,  0.0003, -0.0071, -0.0247, -0.0189,
         0.0251,  0.0054, -0.0122, -0.0062,  0.0170,  0.0088],
       requires_grad=True)), ('linear5.weight', Parameter containing:
tensor([[ 0.2241,  0.1130,  0.3022,  0.1916,  0.2223,  0.0431, -0.3426, -0.3440,
          0.1822, -0.3151, -0.0628,  0.3699, -0.3455, -0.3877]],
       requires_grad=True)), ('linear3.weight', Parameter containing:
tensor([[-1.9147e-01,  2.8014e-01, -1.3991e-01,  4.0160e-01, -2.9750e-01,
         -4.0675e-01, -1.9263e-01, -1.0415e-01, -1.9963e-01, -2.0071e-01,
          1.1691e-02,  9.4754e-02,  9.4819e-02, -2.8988e-01],
        [-4.3435e-01,  1.9047e-01,  1.5905e-02,  6.6229e-02,  4.1638e-01,
          3.2126e-02,  4.1763e-01,  8.3396e-02, -1.7449e-01, -7.6187e-02,
          4.0028e-01,  5.0770e-01, -4.9770e-02, -1.2033e-01],
        [-8.0952e-02, -2.3954e-01,  1.6748e-01,  4.2988e-04,  3.4716e-02,
         -2.4230e-01,  3.6205e-01, -1.9855e-01, -4.4221e-01, -4.3206e-02,
         -6.3973e-02,  1.8759e-01,  3.8555e-01, -1.3367e-02],
        [-4.2937e-01,  3.9707e-01,  4.3481e-01,  6.8181e-02, -4.1383e-01,
          3.0049e-01,  3.2526e-01, -7.9330e-02, -2.5338e-01, -4.2153e-01,
          1.6624e-01, -1.6104e-01,  6.5737e-02, -2.9485e-01],
        [-2.3657e-01,  1.6295e-01, -4.0080e-02, -1.5815e-01, -2.8085e-01,
         -9.0254e-02, -9.5679e-02, -4.0740e-03, -2.3149e-01, -6.2303e-02,
          4.1956e-01, -3.8989e-01,  1.6249e-01, -1.8731e-01],
        [-7.5821e-02, -3.0767e-01, -3.6200e-01,  1.8419e-01,  2.3292e-01,
          1.8993e-01,  2.5734e-01,  1.0526e-02, -2.2383e-02,  2.1955e-01,
          1.8093e-01, -3.4223e-01,  3.4021e-01, -4.1540e-01],
        [ 4.6872e-01, -2.5313e-01,  5.0806e-01,  2.5260e-01,  1.7962e-01,
          6.1036e-02, -1.5670e-01, -1.5870e-01,  6.4256e-02,  1.0272e-01,
          1.4937e-01, -2.0187e-01, -7.3561e-02, -1.5869e-01],
        [-3.3387e-01,  1.6482e-01,  2.9494e-01, -1.9365e-01, -1.8845e-02,
         -3.0961e-01, -3.9860e-01, -8.9242e-02, -2.0225e-02, -2.8819e-01,
         -4.3575e-01, -3.6145e-01,  4.1354e-01, -3.9197e-01],
        [-2.5357e-01, -4.6114e-01, -2.8988e-01, -2.4051e-01,  1.2374e-01,
         -2.3000e-01, -7.7881e-02,  3.2498e-01, -3.0910e-01,  7.9554e-02,
          1.9413e-02,  4.3009e-02, -1.0415e-02, -1.7942e-01],
        [-3.7767e-01, -2.3278e-01,  3.8294e-01,  3.5919e-01,  2.9566e-01,
         -3.5014e-01,  2.3018e-02, -3.7174e-01,  2.4791e-01,  2.4805e-01,
          3.0085e-01, -3.2055e-01,  4.5890e-01, -2.3091e-01],
        [ 2.7055e-01,  1.1920e-01,  1.5884e-01,  2.6455e-01,  2.2785e-01,
          7.6157e-02,  3.6498e-01,  4.8730e-02,  8.1615e-02,  2.5814e-01,
         -4.7729e-01,  1.0518e-01,  4.4344e-01,  1.7768e-01],
        [-1.7698e-01, -1.0043e-01,  4.4959e-01,  3.3477e-01, -6.0899e-02,
          3.5387e-01,  4.1428e-01,  2.9283e-01, -3.9635e-01, -3.0678e-01,
          9.8975e-02, -1.0160e-01, -1.2551e-01,  4.7504e-01],
        [-2.3299e-01,  2.5722e-01,  4.6488e-01,  1.5887e-01, -1.1054e-01,
         -7.4404e-03, -3.8438e-01, -3.0515e-02,  3.8285e-03,  3.6836e-01,
         -4.2468e-02,  2.6934e-02, -4.0358e-01,  3.9799e-01],
        [-4.4207e-01,  3.1176e-01,  2.4388e-01, -8.3642e-02,  1.7519e-01,
         -4.1707e-01, -2.1719e-01, -4.1956e-01,  5.0163e-01,  2.3155e-01,
          3.1532e-01,  2.1522e-01,  3.5177e-01,  8.5299e-02]],
       requires_grad=True))}

torch.Size([3833, 14]) (3833, 1)

[   0    1    2 ... 3830 3831 3832] [[0.04381375]
 [1.0782385 ]]
[[-0.40946546]
 [-0.2648227 ]]
Out[34]:
array([[4.40964181],
       [4.48751214],
       [4.53860294],
       ...,
       [4.29864503],
       [4.29237543],
       [4.28881426]])

lineplot for evaluating targets and model predictions¶

100 epochs training

10 epochs training

Parameter containing:
tensor([[-0.2174, -0.0477,  0.2296, -0.1854, -0.0897, -0.3259,  0.3711,  0.2363,
         -0.2432, -0.0459, -0.2803,  0.3055, -0.5518, -0.0377],
        [-0.1620, -0.0455,  0.4977, -0.1960,  0.1284, -0.1358,  0.0711,  0.1784,
         -0.0842, -0.1122,  0.2479,  0.1767, -0.0245, -0.1172],
        [ 0.1470, -0.0213,  0.2368,  0.0958,  0.0787,  0.3669,  0.3339,  0.2583,
          0.2184, -0.3127,  0.1844, -0.2393,  0.1190, -0.3780],
        [-0.2335, -0.4764, -0.2744, -0.4631,  0.3320, -0.3015, -0.4802, -0.1977,
          0.3239, -0.2276,  0.0225,  0.2525, -0.0237, -0.1719],
        [-0.0829,  0.4307, -0.0146, -0.0816, -0.4764,  0.2676, -0.3845,  0.0192,
         -0.0333, -0.3748,  0.2229, -0.2139,  0.4690, -0.3792],
        [ 0.0107,  0.0662,  0.5012,  0.2476,  0.0143, -0.3019, -0.3472, -0.3025,
         -0.0371, -0.2818, -0.4075,  0.3411,  0.1113, -0.1859],
        [ 0.4187,  0.1496,  0.1810, -0.2980, -0.1732,  0.3150, -0.2772, -0.2243,
         -0.3606, -0.2044, -0.2539, -0.1795, -0.2794, -0.3949],
        [ 0.5943,  0.1195, -0.0291,  0.0088, -0.3794,  0.0766,  0.0711,  0.0794,
          0.0738,  0.0326, -0.3712,  0.3287,  0.0117,  0.2911],
        [ 0.1236,  0.0750, -0.0046,  0.0852,  0.0744,  0.4183,  0.3072, -0.2120,
         -0.4209,  0.0723, -0.3576,  0.3874,  0.4331, -0.3799],
        [ 0.4258,  0.3015,  0.2174,  0.1015, -0.3777,  0.2987,  0.0797,  0.1690,
         -0.1784,  0.2900,  0.2812,  0.2837, -0.1835, -0.0399],
        [-0.2470, -0.1502,  0.1117, -0.4598,  0.3388, -0.0656,  0.2639,  0.3155,
          0.2992,  0.1453, -0.1092,  0.3163,  0.6282,  0.3293],
        [-0.0649,  0.4257, -0.3316,  0.0303, -0.1931,  0.2408, -0.4654,  0.2061,
          0.2694,  0.1945, -0.3103, -0.3968,  0.0809, -0.2380],
        [-0.1983, -0.2313, -0.2305,  0.1027, -0.0205, -0.1703, -0.0589, -0.3306,
         -0.0739, -0.2513,  0.2541,  0.2837,  0.5314,  0.2525],
        [ 0.0582,  0.1564,  0.4340,  0.0440,  0.0998,  0.2344, -0.4467,  0.1417,
         -0.1391, -0.0632, -0.0043,  0.2358,  0.2559,  0.1380]],
       requires_grad=True)
Parameter containing:
tensor([-0.0010,  0.0032,  0.0196, -0.0214, -0.0005,  0.0027, -0.0052,  0.0170,
         0.0078, -0.0191,  0.0115, -0.0210,  0.0071, -0.0034],
       requires_grad=True)
Parameter containing:
tensor([[-0.1420,  0.3804,  0.4161,  0.3425,  0.2254,  0.0583, -0.0991,  0.4611,
          0.1529,  0.2844, -0.3813,  0.0910,  0.1286,  0.4384],
        [ 0.2896, -0.1127, -0.1398,  0.1135, -0.1619, -0.2175,  0.1935,  0.0836,
         -0.0041,  0.0473,  0.0014, -0.0691, -0.3158, -0.1613],
        [-0.3189, -0.2332,  0.2725, -0.1830,  0.4944, -0.0563, -0.1150, -0.2143,
          0.4754, -0.3354,  0.3835,  0.2301,  0.3723, -0.3633],
        [-0.2627, -0.1276,  0.0659,  0.1132, -0.1190, -0.4603, -0.2060,  0.3041,
          0.3216, -0.1978,  0.1061,  0.3034, -0.1455,  0.3624],
        [-0.0100, -0.1756,  0.0884, -0.2744,  0.0583,  0.4709,  0.0184, -0.1844,
         -0.0956, -0.0988, -0.2589, -0.4324,  0.3199, -0.3993],
        [ 0.2218, -0.3123, -0.1992,  0.2801, -0.1229,  0.4241,  0.2832,  0.2738,
          0.1238,  0.0352, -0.0678, -0.4130,  0.4317, -0.3584],
        [-0.0341, -0.1671,  0.0178,  0.3847,  0.0790, -0.0114, -0.0334, -0.2519,
         -0.3461,  0.0279, -0.2257,  0.0119, -0.1657,  0.0379],
        [-0.3844, -0.0326, -0.1544, -0.4082,  0.3465,  0.0098,  0.2029, -0.0744,
          0.4221,  0.4238,  0.3138,  0.1537, -0.3871,  0.3048],
        [-0.0310, -0.2871,  0.2842, -0.4538, -0.1230,  0.4883, -0.3638,  0.3351,
          0.2214,  0.1306, -0.0591, -0.3494, -0.0655, -0.3938],
        [-0.2617,  0.3005,  0.4206,  0.0813, -0.1321, -0.3644, -0.2966, -0.0610,
          0.2565, -0.4343,  0.2658, -0.3859, -0.0156,  0.0210],
        [ 0.4863,  0.1667,  0.3306,  0.0689, -0.4304,  0.2662, -0.0058, -0.2870,
          0.1544, -0.0011, -0.3980,  0.3091,  0.2165, -0.2811],
        [ 0.2488,  0.3122,  0.0024,  0.4402, -0.1951,  0.2958, -0.2055, -0.3801,
         -0.1868, -0.0132, -0.1687,  0.1677, -0.0345,  0.0715],
        [ 0.3554,  0.4615,  0.0218,  0.0107,  0.0345,  0.2140,  0.1369, -0.1263,
         -0.3384, -0.3234, -0.0824, -0.1884, -0.2340,  0.1700],
        [-0.1189,  0.3436,  0.4470, -0.4101,  0.4641,  0.1861,  0.3777,  0.0709,
         -0.2931, -0.1375,  0.0879, -0.4039,  0.1675,  0.3870]],
       requires_grad=True)
Parameter containing:
tensor([ 0.0054,  0.0212,  0.0157,  0.0018,  0.0003, -0.0071, -0.0247, -0.0189,
         0.0251,  0.0054, -0.0122, -0.0062,  0.0170,  0.0088],
       requires_grad=True)
Parameter containing:
tensor([[-1.9147e-01,  2.8014e-01, -1.3991e-01,  4.0160e-01, -2.9750e-01,
         -4.0675e-01, -1.9263e-01, -1.0415e-01, -1.9963e-01, -2.0071e-01,
          1.1691e-02,  9.4754e-02,  9.4819e-02, -2.8988e-01],
        [-4.3435e-01,  1.9047e-01,  1.5905e-02,  6.6229e-02,  4.1638e-01,
          3.2126e-02,  4.1763e-01,  8.3396e-02, -1.7449e-01, -7.6187e-02,
          4.0028e-01,  5.0770e-01, -4.9770e-02, -1.2033e-01],
        [-8.0952e-02, -2.3954e-01,  1.6748e-01,  4.2988e-04,  3.4716e-02,
         -2.4230e-01,  3.6205e-01, -1.9855e-01, -4.4221e-01, -4.3206e-02,
         -6.3973e-02,  1.8759e-01,  3.8555e-01, -1.3367e-02],
        [-4.2937e-01,  3.9707e-01,  4.3481e-01,  6.8181e-02, -4.1383e-01,
          3.0049e-01,  3.2526e-01, -7.9330e-02, -2.5338e-01, -4.2153e-01,
          1.6624e-01, -1.6104e-01,  6.5737e-02, -2.9485e-01],
        [-2.3657e-01,  1.6295e-01, -4.0080e-02, -1.5815e-01, -2.8085e-01,
         -9.0254e-02, -9.5679e-02, -4.0740e-03, -2.3149e-01, -6.2303e-02,
          4.1956e-01, -3.8989e-01,  1.6249e-01, -1.8731e-01],
        [-7.5821e-02, -3.0767e-01, -3.6200e-01,  1.8419e-01,  2.3292e-01,
          1.8993e-01,  2.5734e-01,  1.0526e-02, -2.2383e-02,  2.1955e-01,
          1.8093e-01, -3.4223e-01,  3.4021e-01, -4.1540e-01],
        [ 4.6872e-01, -2.5313e-01,  5.0806e-01,  2.5260e-01,  1.7962e-01,
          6.1036e-02, -1.5670e-01, -1.5870e-01,  6.4256e-02,  1.0272e-01,
          1.4937e-01, -2.0187e-01, -7.3561e-02, -1.5869e-01],
        [-3.3387e-01,  1.6482e-01,  2.9494e-01, -1.9365e-01, -1.8845e-02,
         -3.0961e-01, -3.9860e-01, -8.9242e-02, -2.0225e-02, -2.8819e-01,
         -4.3575e-01, -3.6145e-01,  4.1354e-01, -3.9197e-01],
        [-2.5357e-01, -4.6114e-01, -2.8988e-01, -2.4051e-01,  1.2374e-01,
         -2.3000e-01, -7.7881e-02,  3.2498e-01, -3.0910e-01,  7.9554e-02,
          1.9413e-02,  4.3009e-02, -1.0415e-02, -1.7942e-01],
        [-3.7767e-01, -2.3278e-01,  3.8294e-01,  3.5919e-01,  2.9566e-01,
         -3.5014e-01,  2.3018e-02, -3.7174e-01,  2.4791e-01,  2.4805e-01,
          3.0085e-01, -3.2055e-01,  4.5890e-01, -2.3091e-01],
        [ 2.7055e-01,  1.1920e-01,  1.5884e-01,  2.6455e-01,  2.2785e-01,
          7.6157e-02,  3.6498e-01,  4.8730e-02,  8.1615e-02,  2.5814e-01,
         -4.7729e-01,  1.0518e-01,  4.4344e-01,  1.7768e-01],
        [-1.7698e-01, -1.0043e-01,  4.4959e-01,  3.3477e-01, -6.0899e-02,
          3.5387e-01,  4.1428e-01,  2.9283e-01, -3.9635e-01, -3.0678e-01,
          9.8975e-02, -1.0160e-01, -1.2551e-01,  4.7504e-01],
        [-2.3299e-01,  2.5722e-01,  4.6488e-01,  1.5887e-01, -1.1054e-01,
         -7.4404e-03, -3.8438e-01, -3.0515e-02,  3.8285e-03,  3.6836e-01,
         -4.2468e-02,  2.6934e-02, -4.0358e-01,  3.9799e-01],
        [-4.4207e-01,  3.1176e-01,  2.4388e-01, -8.3642e-02,  1.7519e-01,
         -4.1707e-01, -2.1719e-01, -4.1956e-01,  5.0163e-01,  2.3155e-01,
          3.1532e-01,  2.1522e-01,  3.5177e-01,  8.5299e-02]],
       requires_grad=True)
Parameter containing:
tensor([-0.0025, -0.0077, -0.0057, -0.0073,  0.0109, -0.0125,  0.0121,  0.0202,
        -0.0285,  0.0046,  0.0167, -0.0016,  0.0065,  0.0130],
       requires_grad=True)
Parameter containing:
tensor([[ 0.1714,  0.1197,  0.0330,  0.1618, -0.2151,  0.1414,  0.1899,  0.1656,
         -0.0549,  0.2844, -0.0739, -0.2121, -0.0520,  0.0149],
        [ 0.2081, -0.2049, -0.0494, -0.0862,  0.1835,  0.1723,  0.2691,  0.2454,
         -0.1328,  0.2680,  0.1822, -0.1541,  0.2091,  0.2039],
        [ 0.0082,  0.1312, -0.1129, -0.0305, -0.1256, -0.1301, -0.0060,  0.2429,
          0.2288,  0.0901, -0.1780, -0.2241,  0.0952,  0.1636],
        [-0.1290, -0.1019,  0.2428, -0.1472, -0.0250,  0.0081,  0.2377,  0.0191,
         -0.0550, -0.0321, -0.2413,  0.0807,  0.0926, -0.1268],
        [ 0.1914, -0.0724,  0.0591, -0.0411,  0.1717,  0.0010,  0.0359,  0.2572,
         -0.1532, -0.2171,  0.1327, -0.0515,  0.2842, -0.3202],
        [ 0.1614,  0.0544, -0.2580,  0.0157,  0.0379,  0.0778, -0.1868,  0.2161,
         -0.0525, -0.2308,  0.1820,  0.0329, -0.1009,  0.1778],
        [-0.0903, -0.1353, -0.2056, -0.2771,  0.2050,  0.1043, -0.0293,  0.1621,
         -0.1869,  0.1222,  0.2350,  0.1508, -0.1821,  0.2834],
        [ 0.2688, -0.0510,  0.1625, -0.1706, -0.2369,  0.0368, -0.2710,  0.1567,
          0.2810, -0.1745, -0.2284, -0.0040, -0.1609,  0.0600],
        [ 0.1307,  0.0658,  0.0721,  0.2496, -0.0610,  0.1338,  0.1015,  0.0185,
          0.1613,  0.2644, -0.0798, -0.0863,  0.2370,  0.2095],
        [ 0.2089,  0.2733,  0.0730,  0.2533,  0.0299, -0.0084, -0.1657, -0.1189,
         -0.2565,  0.1682,  0.2050, -0.0829, -0.2530, -0.0889],
        [ 0.1045,  0.1494,  0.1488,  0.0423, -0.0553,  0.2152,  0.1122,  0.2012,
         -0.2202,  0.1824, -0.0763, -0.0237, -0.2069,  0.0269],
        [-0.0013, -0.2133, -0.0338,  0.0984,  0.1568, -0.2447,  0.0426,  0.0012,
          0.0676, -0.1821,  0.2396,  0.2206,  0.3121, -0.2286],
        [ 0.1062, -0.1704,  0.1417, -0.2392, -0.0706, -0.2622, -0.0825,  0.1712,
         -0.0053, -0.2546, -0.1470, -0.1186,  0.1783,  0.1717],
        [ 0.1974,  0.2851,  0.2093,  0.0514, -0.0472,  0.2102, -0.3419,  0.1228,
          0.1453,  0.0385,  0.2584, -0.1215, -0.1840, -0.2062]],
       requires_grad=True)
Parameter containing:
tensor([ 0.1178, -0.0455,  0.1218,  0.1181,  0.2027, -0.2611, -0.1499,  0.0352,
         0.0837,  0.1989, -0.0953,  0.2590,  0.0767,  0.1373],
       requires_grad=True)
Parameter containing:
tensor([[ 0.2241,  0.1130,  0.3022,  0.1916,  0.2223,  0.0431, -0.3426, -0.3440,
          0.1822, -0.3151, -0.0628,  0.3699, -0.3455, -0.3877]],
       requires_grad=True)
Parameter containing:
tensor([-0.1055], requires_grad=True)
Out[39]:
[None, None, None, None, None, None, None, None, None, None]