Table of Contents

• 1  Italian waterbodies data: water source Lupa
  • 1.1  Data set description
    • 1.1.1  Aquifer
    • 1.1.2  Water spring
    • 1.1.3  River Arno
    • 1.1.4  Lake Bilancino
  • 1.2  Introduction
  • 1.3  Methodology
• 2  Water spring Lupa
  • • 2.0.1  References
    • 2.0.2  Evolution of the outflow over the last 11 years
  • 2.1  taking the differences
    • 2.1.1  logarithms of the flow rate.
    • 2.1.2  pmdArima: introduction
      • 2.1.2.1  2020
  • 2.2  Rainfall
    • 2.2.1  Annual Water Budget Ratio (AWBR)
  • 2.3  Arrone rainfall addition
    • 2.3.1  Ancaiano daily pluviometry
      • 2.3.1.1  Ancaiano pluviometry 2009 and 2020-2022
    • 2.3.2  SPI
      • 2.3.2.1  SPI 12 calculation via module standard-precip
      • 2.3.2.2  SPEI
    • 2.3.3  Soil moisture condition
    • 2.3.4  TR-55: 'Urban Hydrology for Small Watersheds'
    • 2.3.5  SCS CN- or curve number method
      • 2.3.5.1  Runoff Equation
      • 2.3.5.2  SCS Hydrologic Soil Groups: Soil textures
    • 2.3.6  Runoff curve numbers for cultivated/other agricultural lands and soil types
    • 2.3.7  Curve-number map for Umbria Region
    • 2.3.8  Calculate runoff depth
    • 2.3.9  The determination of CN values: by formula method, or by conversion table method
  • 2.4  Infiltration coefficients method
    • 2.4.1  Calculate the infiltrate amount i.f.o mm/day rainfall
  • 2.5  Temperature
    • 2.5.1  Heat index per year
    • 2.5.2  T2M_MAX, T2M_MIN, relative humidity
    • 2.5.3  AET/PET - Drought Index
  • 2.6  Flow rate original data
    • 2.6.1  Rolling sums monthly
    • 2.6.2  The variability index (Meinzer, 1927)
    • 2.6.3  First attempt to gather better flow rate data...
    • 2.6.4  resample flow rate 2010-2019 monthly
    • 2.6.5  The 2012 series
    • 2.6.6  Maximum 1999-2011, Minimum 1999-2011, Mean 1999-2011
    • 2.6.7  Mean of period 2010-2020 vs. the Mean of 1999-2011
      • 2.6.7.1  Set list of distributions to test
    • 2.6.8  Conversion of units etc...
    • 2.6.9  Yearly and monthly aggregates
      • 2.6.9.1  statsmodels api
      • 2.6.9.2  Netto infiltration - outflow
    • 2.6.10  statsmodels SARIMAX
  • 2.7  pmdArima examples
    • 2.7.1  Fitting an auto_arima model
    • 2.7.2  Displaying key timeseries statistics
    • 2.7.3  Array differencing
    • 2.7.4  Modeling quasi-seasonal trends with date features
    • 2.7.5  Rolling sums in m³
      • 2.7.5.1  Rainfall rolling sums
      • 2.7.5.2  Cumulative sums for the rainfall and outflow in cubic meters.
      • 2.7.5.3  Water balance m³ rainfall - water spring outflow
    • 2.7.6  Cross-correlation and Auto-correlation
      • 2.7.6.1  Cross-correlation daily and weekly data
      • 2.7.6.2  Cross-correlation daily and weekly data
    • 2.7.7  Recession coefficient or coefficient of depletion
    • 2.7.8  Plots of absolute vs. mean values of Q / t
    • 2.7.9  Outflow of 2017
    • 2.7.10  Calculating evapotranspiration method 1
    • 2.7.11  Calculating evapotranspiration method 2
    • 2.7.12  Evapotranspiration water spring Peschiera
  • 2.8  Solar Radiation
    • 2.8.1  Hargreaves method
      • 2.8.1.1  Simplification through the relation T_avg - T_max - T_min
      • 2.8.1.2  W/m² to MJ/m²
      • 2.8.1.3  extract T_max - T_min for Hargreaves formula method
  • 2.9  Random forest regression with XGBoost
    • 2.9.1  based on poor data
    • 2.9.2  Predictions based on much better data
    • 2.9.3  We try the 'best' dataset here
    • 2.9.4  We try the 'best' dataset here [2]: TimeSeriesSplit
  • 2.10  Prediction of flow rate of the source
    • 2.10.1  Random Forest Regressor (sklearn)
      • 2.10.1.1  Permutation Feature Importance
      • 2.10.1.2  RF regressor metrics
      • 2.10.1.3  RF regressor predictions vs. observations
      • 2.10.1.4  Predictionplot: Lupa source flow rate
      • 2.10.1.5  Method 2 to compare results
      • 2.10.1.6  Time-related feature engineering: Trigonometric_features
    • 2.10.2  ExtraTreesRegressor
      • 2.10.2.1  ET regressor metrics
      • 2.10.2.2  ET regressor: predictions vs. observations
      • 2.10.2.3  Predictionplot: observed vs. estimated source flow rate
  • 2.11  Revisiting the Lupa data
    • • 2.11.0.1  2009 and 2020-2022 debit data
    • 2.11.1  Calculation of the recession coefficients α over a span of several days.
    • 2.11.2  determination of Correlation coefficients rain-outflow
      • 2.11.2.1  Rainfall_Terni vs infiltrate comparison
      • 2.11.2.2  Outflow data of 2009 and 2020-2021:
      • 2.11.2.3  Correlations: monthly shifted
  • 2.12  Alternative approach of considering P5 in the SCS-CN model
  • 2.13  The older and more recent water spring parameters in overview table.
    • • 2.13.0.1  The slope of the recession curve vs. maximum outflow

Italian waterbodies data: water source Lupa

Can you help preserve "blue gold" using data to predict water availability?
Acea Smart Water Analytics

https://www.kaggle.com/c/acea-water-prediction/data

Data set description

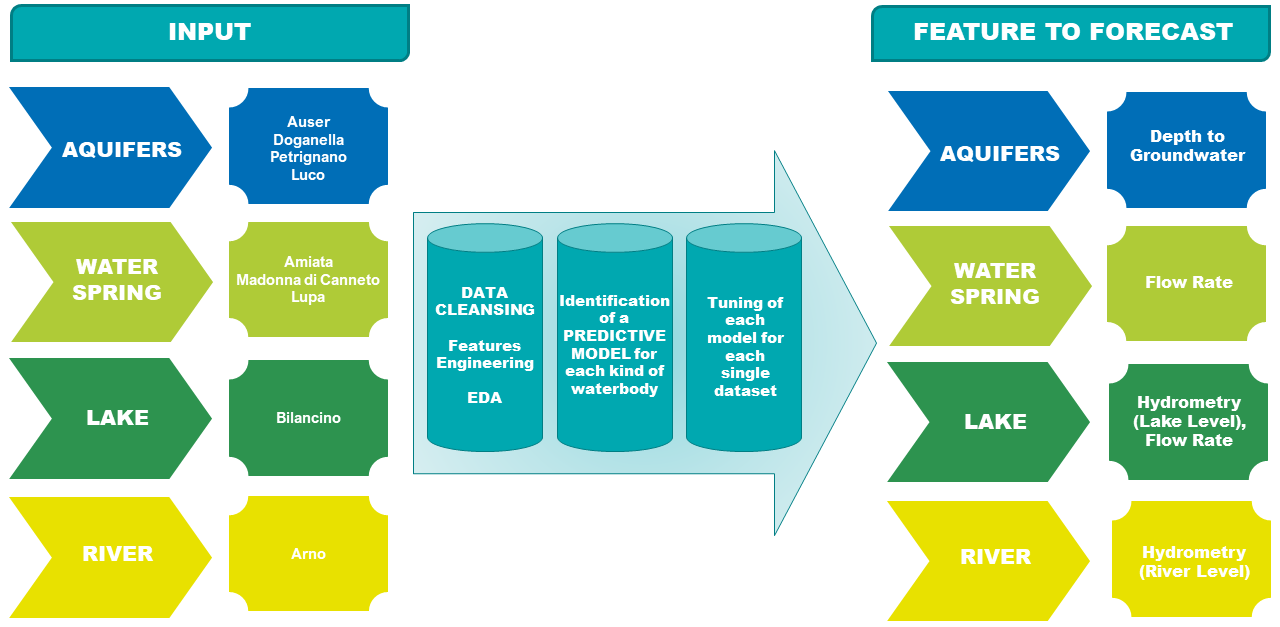
This competition uses nine different datasets, completely independent and not linked to each other. Each dataset can represent a different kind of waterbody. As each waterbody is different from the other, the related features as well are different from each other. So, if for instance we consider a water spring we notice that its features are different from the lake’s one. This is correct and reflects the behavior and characteristics of each waterbody. The Acea Group deals with four different type of waterbodies: water spring (for which three datasets are provided), lake (for which a dataset is provided), river (for which a dataset is provided) and aquifers (for which four datasets are provided).

Let’s see how these nine waterbodies differ from each other.

Aquifer

Auser

• This waterbody consists of two subsystems, called NORTH and SOUTH, where the former partly influences the behavior of the latter. Indeed, the north subsystem is a water table (or unconfined) aquifer while the south subsystem is an artesian (or confined) groundwater. The levels of the NORTH sector are represented by the values of the SAL, PAG, CoS and DIEC wells, while the levels of the SOUTH sector by the LT2 well.

Petrignano Aquifer

• The wells field of the alluvial plain between Ospedalicchio di Bastia Umbra and Petrignano is fed by three underground aquifers separated by low permeability septa. The aquifer can be considered a water table groundwater and is also fed by the Chiascio river. The groundwater levels are influenced by the following parameters: rainfall, depth to groundwater, temperatures and drainage volumes, level of the Chiascio river.

Doganella Aquifer

• The wells field Doganella is fed by two underground aquifers not fed by rivers or lakes but fed by meteoric infiltration. The upper aquifer is a water table with a thickness of about 30m. The lower aquifer is a semi-confined artesian aquifer with a thickness of 50m and is located inside lavas and tufa products. These aquifers are accessed through wells called Well 1, ..., Well 9. Approximately 80 \% of the drainage volumes come from the artesian aquifer. The aquifer levels are influenced by the following parameters: rainfall, humidity, subsoil, temperatures and drainage volumes.

Luco Aquifer

• The Luco wells field is fed by an underground aquifer. This aquifer not fed by rivers or lakes but by meteoric infiltration at the extremes of the impermeable sedimentary layers. Such aquifer is accessed through wells called Well 1, Well 3 and Well 4 and is influenced by the following parameters: rainfall, depth to groundwater, temperature and drainage volumes.

Water spring

Amiata

• The Amiata waterbody is composed of a volcanic aquifer not fed by rivers or lakes but fed by meteoric infiltration. This aquifer is accessed through Ermicciolo, Arbure, Bugnano and Galleria Alta water springs. The levels and volumes of the four sources are influenced by the parameters: rainfall, depth to groundwater, hydrometry, temperatures and drainage volumes.

Madonna di Canneto

• The Madonna di Canneto spring is situated at an altitude of 1010m above sea level in the Canneto valley. It does not consist of an aquifer and its source is supplied by the water catchment area of the river Melfa.
• Settefrati is a commune with an altitude of 784 m and surface area of 50,6 km².

Lupa

• This water spring is located in the Rosciano Valley, on the left side of the Nera river. The waters emerge at an altitude of about 375 meters above sea level through a long draining tunnel that crosses, in its final section, lithotypes and essentially calcareous rocks. It provides drinking water to the city of Terni and the towns around it.

River Arno

• Arno is the second largest river in peninsular Italy and the main waterway in Tuscany and it has a relatively torrential regime, due to the nature of the surrounding soils (marl and impermeable clays). Arno results to be the main source of water supply of the metropolitan area of Florence-Prato-Pistoia. The availability of water for this waterbody is evaluated by checking the hydrometric level of the river at the section of Nave di Rosano.

Lake Bilancino

• Bilancino lake is an artificial lake located in the municipality of Barberino di Mugello (about 50 km from Florence). It is used to refill the Arno river during the summer months. Indeed, during the winter months, the lake is filled up and then, during the summer months, the water of the lake is poured into the Arno river.

Each waterbody has its own different features to be predicted. The table below shows the expected feature to forecast for each waterbody.

It is of the utmost importance to notice that some features like rainfall and temperature, which are present in each dataset, don’t go alongside the date. Indeed, both rainfall and temperature affect features like level, flow, depth to groundwater and hydrometry some time after it fell down. This means, for instance, that rain fell on 1st January doesn’t affect the mentioned features right the same day but some time later. As we don’t know how many days/weeks/months later rainfall affects these features, this is another aspect to keep into consideration when analyzing the dataset.

A short, tabular description of the waterbodies is available also downloading all datasets.

More information about the behavior of each kind of waterbody can be found at the following links:

• Aquifer https://en.wikipedia.org/wiki/Aquifer
• Water spring https://en.wikipedia.org/wiki/Spring_(hydrology)
• River https://en.wikipedia.org/wiki/River
• Lake https://en.wikipedia.org/wiki/Lake

C:\Users\VanOp\AppData\Local\Temp\ipykernel_15916\1212899292.py:14: DeprecationWarning: Importing display from IPython.core.display is deprecated since IPython 7.14, please import from IPython display
  from IPython.core.display import display, HTML, SVG

Autosaving every 500 seconds

---

'%.4f'

Introduction

In recent years, long and frequent droughts have affected many countries in the world. These events require an ever more careful and rational management of water resources. Most of the globe’s unfrozen freshwater reserves are stored in aquifers. Groundwater is generally a renewable resource that shows good quality and resilience to fluctuations. Thus, if properly managed, groundwater could ensure long-term supply in order to meet increasing water demand.

For this purpose, it is of crucial importance to be able to predict the flow rates provided by springs. These represent the transitions from groundwater to surface water and reflect the dynamics of the aquifer, with the whole flow system behind. Moreover, spring influences water bodies into which they discharge. The importance of springs in groundwater research is highlighted in some significant contributions. In-depth studies on springs started only after the concept of sustainability was introduced in the management of water resources.

A spring hydrograph is the consequence of several processes governing the transformation of precipitation in the spring recharge area into the single output discharge at the spring. A water balance states that the change rate in water stored in the feeding aquifer is balanced by the rate at which water flows into and out of the aquifer. A quantitative water balance generally has to take the following terms into account: precipitation, infiltration, surface runoff, evapotranspiration, groundwater recharge, soil moisture deficit, spring discharge, lateral inflow to the aquifer, leakage between the aquifer and the underlying aquitard, well pumpage from the aquifer, and change of the storage in the aquifer.

In many cases, the evaluation of the terms of the water balance is very complicated. The complexity of the problem arises from many factors: hydrologic, hydrographic, and hydrogeological features, geologic and geomorphologic characteristics, land use, land cover, water withdrawals, and climatic conditions.

Even more complicated would be to estimate future spring discharges by using a model based on the balance equations. Therefore, simplified approaches are frequently pursued for practical purposes.

Many authors have addressed the problem of correlating the spring discharges to the rainfall through different approaches...

Methodology

The Methodology to use depends on the properties of the water source, local geology, and the unknown parameters. There is no clear cut path.
An example of a methodology is presented in the next illustration. It provides a view how the topics I handled are related to each other, and how unknown info and truthfull data matters to obtain a reasonable result.

Water spring Lupa

<!img src="http://vanoproy.be/css/Lupa.jpg"-->

432000 l/h 10368000 l/d

Nella dorsale montuosa che occupa la parte orientale della regione, esistono due sistemi idrogeologici separati dalla linea tettonica denominata “linea della Valnerina”, dove è individuabile un limite di permeabilità che corre a quote variabili tra 350 e 700 m s.l.m.: a sud il “Sistema della Valnerina” e a nord il “Sistema dell’Umbria nord-orientale”.
Con “Sistema della Valnerina”, viene identificata l’imponente struttura idrogeologica presente al margine sud-orientale del territorio regionale. Questa si estende dal corso del Fiume Nera, ad ovest, fino alla linea tettonica Ancona-Anzio, la sua superficie in territorio umbro è di circa 1.100 km2. Il sistema nel suo complesso è caratterizzato dalla presenza di una serie di acquiferi costituiti principalmente dalle formazioni della Scaglia s.l., della Maiolica e della Corniola-Calcare Massiccio. Questi presentano comunque continuità idraulica sia per contatti laterali che verticali. La formazione della Scaglia s.l. ospita l’acquifero più superficiale, che dà luogo a sorgenti puntuali per lo più di modesta portata e contribuisce all’alimentazione del deflusso di base dei corsi d’acqua o alla ricarica degli acquiferi più profondi.
I livelli piezometrici raggiungono quote superiori a 800 m s.l.m. e decrescono da est ad ovest fino a raggiungere la minima quota in corrispondenza dell'alveo del Nera, che costituisce il livello di base principale del sistema. Lungo questa linea di drenaggio dominante, diretta SO-NE, si hanno importanti sorgenti lineari responsabili di notevoli incrementi di portata del fiume Nera. Studi pregressi hanno stimato che, lungo il tratto umbro del fiume Nera, si hanno emergenze in alveo per una portata media complessiva superiore a 15 m3 al secondo. Oltre alle emergenze in alveo, si trovano numerose sorgenti localizzate, che rilasciano una frazione molto più modesta delle acque della struttura, valutabile in qualche centinaio di litri al secondo. Le restituzioni sorgentizie, di tipo sia lineare sia puntuale, sono stimate in un volume di circa 700 Mm3 annui.

The Lupa water spring is located in the central Apennines range on the left side of the river Nera near Arenno, and has an historical flowrate of about 120 l/sec. The aquifer of this karstic system contains deposits named Scaglia. The net recharge of the "Scaglia Calcarea" complex proved to be 170-425 mm/year.
The hydrological unit is called "Monte Coscerno", which has an infiltration efficiency estimated at 475 mm per year based on data from 1997-2007.
Monte Coscerno feeds several waterbodies: the river Nera, the stream F. di Castellone, and 3 notable continuous water springs. The infiltration efficiency increases going from North to South.

Spring	Elevation	Outflow (l/s)
Scheggino	300	200
Lupa	365	125
Pacce	475	80
Castellone	450-325	115

The combined outflow of all the waterbodies of the Monte Coscerno system is +-:

3615 Lupa: 3.46 %, estimated drainage area: 8.3333

520 Lupa: 24 %

Update on estimated drainage area:

• a study from 1996 estimates Lupa's drainage area 10-12 km².
• however it was not mentioned if this value relates to the short term, middle or long term "outflow component" related to 3 waterbearing layers. But I assume it would be short term, which is the most responsive layer.

Location 42.5800 N 12.8132 E
Soils of Italy

References

• Linee Guida sugli Indicatori di Siccità e Scarsità Idrica da utilizzare nelle attività degli Osservatori Permanenti per gli Utilizzi Idrici - Stato Attuale e Prospettive Future (in...), Stefano Mariani, Emanuele Romano,Italian National Research, Giovanni Braca,Barbara Lastoria, Institute for Environmental Protection and Research. Technical Report · June 2018
• SPRINGS (Classification, function,capturing), Soulios G., Dep. of Geology, Aristotle University of Thessaloniki, Bulletin of the Geological Society of Greece, Vol. 43, (2010), DOI: 10.12681/bgsg.11174
• Urban hydrology for small watersheds. Tech. Release 55., U.S. Department of Agriculture, Soil Conservation Service. 1986.
• RUNOFF CURVE NUMBER METHOD: Examination of the Initial Abstraction Ratio, Richard H. Hawkins, Professor, University of Arizona, Tucson, (USDA, Natural Resources Conservation Service, 2002)
• Chapter 20 - Watershed Yield, Part 630 Hydrology, National Engineering Handbook, 2009, USDA
• Groundwater - Hydrology of springs, Chapter 4 - Spring discharge hydrograph, Neven Kresic, Amec Foster Wheeler, Bonacci o., Univ Split Croatia, (2010)
• Karst Groundwater Availability and Sustainable Development, F. Fiorillo, V. Ristić Vakanjac, I. Jemcov, S. P Milanovic, University of Belgrade, February 2015), DOI: 10.1007/978-3-319-12850-4_15
• Predicted Maps for Soil Organic Matter Evaluation: The Case of Abruzzo Region (Italy). Piccini, C.; Francaviglia, R.; Marchetti, A., Land 2020, 9, 349. https://doi.org/10.3390/land9100349
• Machine Learning Models for Spring Discharge Forecasting, Francesco Granata , Michele Saroli, Giovanni de Marinis, and Rudy Gargano, 2018, https://doi.org/10.1155/2018/8328167
• Comparison of antecedent precipitation based rainfall-runoff models, Pankaj Upreti; C. S. P. Ojha, Water Supply (2021) 21 (5): 2122–2138.
• Effective infiltration variability in the Umbria-Marche carbonate aquifers of central Italy, Lucia Mastrorillo, Marco Petitta - Journal of Mediterranean Earth Sciences 2 (2010), 9-18, doi:10.3304/JMES.2010.002

• Water Balance and Soil Moisture Deficit of Different Vegetation Units under Semiarid Conditions in the Andes of Southern Ecuador - Andreas Fries, Karen Silva, Franz Pucha-Cofrep, Fernando Oñate-Valdivieso and Pablo Ochoa-Cueva; Climate 2020, 8(2), 30; https://doi.org/10.3390/cli8020030

• The "APEX" Agricultural Policy Environmental eXtender Model theoretical documentation, Version 0604, BREC Report # 2008-17.

• Fraction of Absorbed Photosynthetically Active Radiation https://land.copernicus.eu/global/products/fapar

	Date	Rainfall_Terni	Flow_Rate_Lupa
0	01/01/2009	2.8	NaN
1	02/01/2009	2.8	NaN
2	03/01/2009	2.8	NaN
3	04/01/2009	2.8	NaN
4	05/01/2009	2.8	NaN

I started with the original dataset of ACEA, which only had errorprone flowrate data for uncomplete 3 years. So I felt I was forced to find better data, which I found on some Italian websites. Later I'd merge the original with the missing flow rate data. But after completing that, the monthly rainfall data was no longer good enough. Moreover this was Terni pluvio data, which is 11 km away from Lupa, plus it is located on the wrong side of the waterbody.
In short: I collected new meaningfull data, and gradually created a new data set

	Date	Rainfall_Terni	Flow_Rate_Lupa	doy	Month	Year	ET01	Infilt_	Infiltsum	Rainfall_Ter	Flow_Rate_Lup	Infilt_m3
0	2009-01-01	2.8	135.47	1.0	1.0	2009.0	NaN	NaN	NaN	352422.0	11704.61	NaN
1	2009-01-02	2.8	135.24	2.0	1.0	2009.0	NaN	NaN	NaN	352422.0	11684.74	NaN
2	2009-01-03	2.8	135.17	3.0	1.0	2009.0	NaN	NaN	NaN	352422.0	11678.69	NaN
3	2009-01-04	2.8	134.87	4.0	1.0	2009.0	NaN	NaN	NaN	352422.0	11652.77	NaN
4	2009-01-05	2.8	134.80	5.0	1.0	2009.0	NaN	NaN	NaN	352422.0	11646.72	NaN

	Date	Rainfall_Terni	Flow_Rate_Lupa	doy	Month	Year	ET01	Infilt_	Infiltsum	Rainfall_Ter	Flow_Rate_Lup	Infilt_m3	Week
0	2010-01-01	3.27	82.24	1.0	1.0	2010.0	1.34	1.93	1.93	412398.0	7105.54	143639.37	53
1	2010-01-02	3.27	88.90	2.0	1.0	2010.0	1.70	1.57	3.51	412398.0	7680.96	130966.87	53
2	2010-01-03	3.27	93.56	3.0	1.0	2010.0	0.94	2.33	5.84	412398.0	8083.58	157582.00	53
3	2010-01-04	3.27	96.63	4.0	1.0	2010.0	1.00	2.28	8.12	412398.0	8348.83	155554.40	1
4	2010-01-05	3.27	98.65	5.0	1.0	2010.0	1.28	1.99	10.11	412398.0	8523.36	145736.74	1

	Rainfall_Terni	Flow_Rate_Lupa	doy	Month	Year	ET01
Date
2010-01-01	3.27	82.24	1	1	2010	1.34
2010-01-02	3.27	88.90	2	1	2010	1.70
2010-01-03	3.27	93.56	3	1	2010	0.94
2010-01-04	3.27	96.63	4	1	2010	1.00
2010-01-05	3.27	98.65	5	1	2010	1.28
2010-01-06	3.27	102.15	6	1	2010	1.21

	Rainfall_Terni	Flow_Rate_Lupa	doy	Month	Year	ET01
Date
2020-06-25	0.0	74.29	177	6	2020	4.03
2020-06-26	0.0	73.93	178	6	2020	4.17
2020-06-27	0.0	73.60	179	6	2020	4.45
2020-06-28	0.0	73.14	180	6	2020	4.51
2020-06-29	0.0	72.88	181	6	2020	4.51
2020-06-30	0.0	72.53	182	6	2020	4.88

<class 'pandas.core.frame.DataFrame'>
DatetimeIndex: 4199 entries, 2009-01-01 to 2020-06-30
Freq: D
Data columns (total 6 columns):
 #   Column          Non-Null Count  Dtype  
---  ------          --------------  -----  
 0   Rainfall_Terni  4199 non-null   float64
 1   Flow_Rate_Lupa  4199 non-null   float64
 2   doy             4199 non-null   int64  
 3   Month           4199 non-null   int64  
 4   Year            4199 non-null   int64  
 5   ET01            3834 non-null   float64
dtypes: float64(3), int64(3)
memory usage: 229.6 KB

This is data I retrieved from an Italian site which had historical (pré 2010) data about Lupa.

	Portata
Data
2009-01-01	135.47
2009-01-02	135.24
2009-01-03	135.17
2009-01-04	134.87
2009-01-05	134.80

	Portata
Data
2010-12-18	189.60
2010-12-19	NaN
2010-12-20	191.03

<class 'pandas.core.frame.DataFrame'>
DatetimeIndex: 4480 entries, 2009-01-01 to 2021-04-07
Freq: D
Data columns (total 1 columns):
 #   Column   Non-Null Count  Dtype  
---  ------   --------------  -----  
 0   Portata  4362 non-null   float64
dtypes: float64(1)
memory usage: 199.0 KB

We need interpolation to fill up some missing gaps due to data for: 23/05/2018 228,70 13/07/2018 179,22 etc...